Thema: Berechnung von Momenten und Kräften | September 2022,
heute beschäftigen wir uns mit der Berechnung von statischen und dynamischen Kraftmomenten (Lastmomenten). Anhand dieser einfachen Berechnungen können wir bestimmen, ob die ausgewählten Linearmotoren die beste Eignung für die Anwendung haben, die wir entwickeln.
Berechnung der statischen Kraft
Beispiel:
Wenn wir eine Masse von 10 kg auf eine Fläche stellen, dann übt diese eine statische Kraft von 98N (10 x 9,8 = 98 N) aus.
Wir beginnen mit dieser physikalischen Größe und wenden dafür die 1. Formel an.
F = m x g
Dabei ist
F – Kraft in N
m – Masse in kg
g – Erdbeschleunigung m/s2
Beispiel:
Wenn wir eine Masse von 10 kg auf eine Fläche stellen, dann übt diese eine statische Kraft von 98N (10 x 9,8 = 98 N) aus.
Berechnung der dynamischen Kraft
Für die Berechnung der dynamischen Kraft ersetzen wir g (Erdbeschleunigung) durch A (Beschleunigung). Hier ist es wichtig zu wissen, dass diese Beschleunigung in dieselbe Richtung wie die Masse wirken muss.
F = m x a
Dabei ist
F – Kraft in N
m – Masse in kg
a – Beschleunigung in m/s2
Beispiel:
Wenn wir eine Masse von 10 kg auf eine Fläche stellen und diese in vertikale Richtung beschleunigen (a = 5 m/s2), dann übt sie eine dynamische Kraft von 50N (10 x 5 = 50 N) aus.
Berechnung der statischen und der dynamischen Kraft zusammen
Nehmen wir an, wir müssen die Kraft berechnen, die ein Aufzug auf das Tragwerk eines Gebäudes ausübt, wenn dieser vertikal verfährt.
Daten:
Masse des Aufzugs: 1000 kg
Beschleunigung: 4,5 m/s2
F = m x a + m x g = 1000 x 4,5 + 1000 x 9,8 = 4500+9800 = 14300 N
Berechnung des statischen Moments
Zur Berechnung des statischen Moments wenden wir folgende Formel an:
M = m x g x X
Dabei ist:
M – das Drehmoment in Nm
X – der Abstand zwischen dem Zentrum der Masse und der Halterung in m
m – die Masse in kg
g – die Erdbeschleunigung in m/s2
Beispiel:
Wenn wir eine Masse von 10 kg in einem Abstand von 300 mm auf eine Fläche stellen, dann wirkt ein statisches Moment von 29,4 Nm (10 x 9,8 x 0,3 = 29,4 Nm). Die Abbildung 1 ist ein Beispiel für die Anwendung.

Berechnung des dynamischen Moments
Zur Berechnung des dynamischen Moments wenden wir folgende Formel an:
M = m x a x X
Dabei ist:
M – das Drehmoment in Nm
X – der Abstand zwischen dem Zentrum der Masse und der Halterung in m
m – die Masse in kg
a – Beschleunigung in m/s2
Beispiel:
Wenn wir eine Masse von 10 kg im Abstand von 300 mm auf einen verfahrbaren Wagen stellen und diesen Wagen außerdem mit einer Beschleunigung von 15 m/s2 bewegen, dann wirkt ein dynamisches Moment von 45 Nm (10 x 15 x 0,3 = 45 Nm).
Die Abbildung 2 zeigt ein Anwendungsbeispiel.
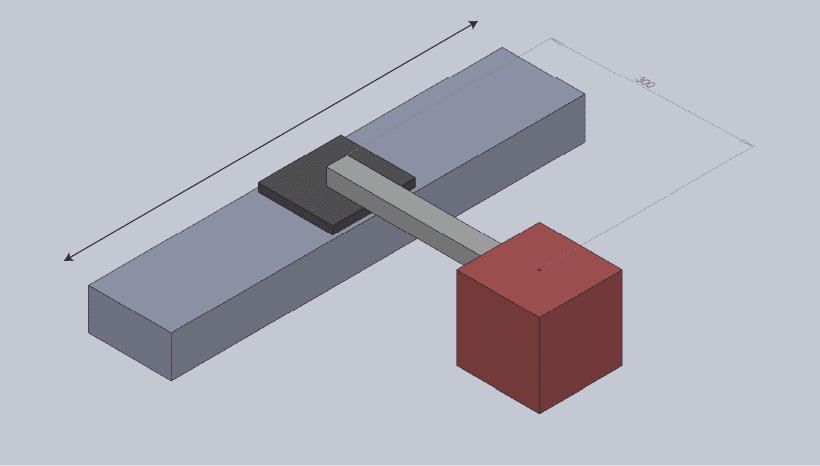
Berechnung der Kräfte sowie der statischen und der dynamischen Momente zusammen
Schauen wir uns ein Beispiel an, bei dem wir die statischen sowie die dynamischen Kräfte und Momente berechnen. Wir setzen dafür die Daten aus den beiden vorstehenden Beispielen an und halten uns an die Reihenfolge laut Abbildung 3.

In diesem Fall haben wir:
Statische Lasten und Momente:
Fz = 98 N
Mx = 29,4 Nm
Dynamische Lasten und Momente:
Mz = 45 Nm
Maximal zulässiger Lastfaktor
Nehmen wir einmal an, dass wir ein Linearmodul MLE30420 für unsere Anwendung ausgewählt haben und die Lastmomente überprüfen müssen. In der nachstehenden Abbildung sind die Katalogwerte für das Modul mit dem Linearmotor MLE30420HS aufgeführt:
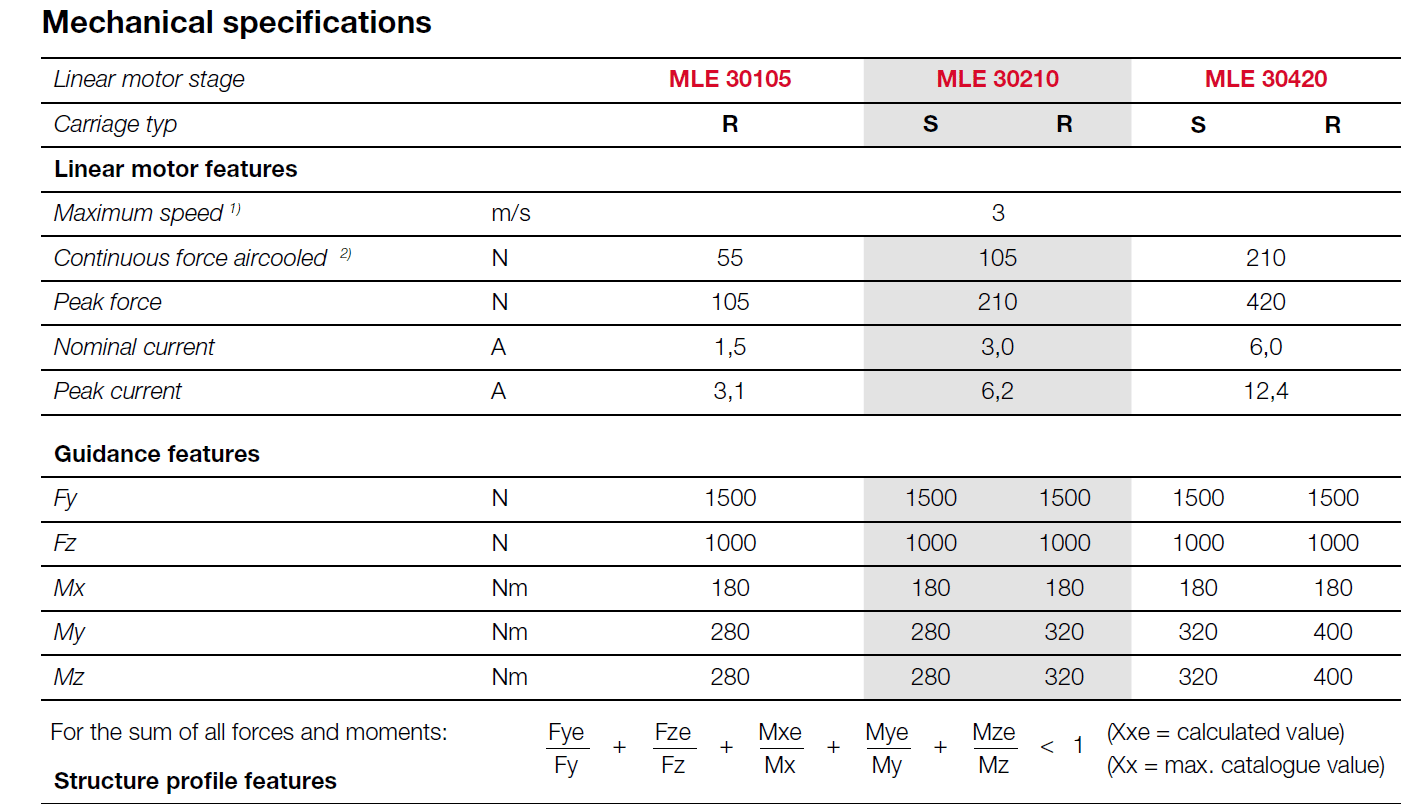
Nun nehmen wir die im Katalog angegebene Formel:
Fy/Fycat + Fz/Fzcat + Mx/Mxcat + My/Mycat + Mz/Mzcat ≤ 1
Oben tragen wir die in den Kapiteln 1, 4 und 5 errechneten Werte ein, und unten die Werte aus dem Katalog. Somit erhalten wir folgendes Ergebnis:
98/1500 + 29.4/180 + 45/320 = 0,07 + 0,16 + 0,14 = 0,23
Wir stellen fest, dass das Ergebnis ≤ 1 ist und haben damit den Nachweis für einen guten Sicherheitsspielraum. Laut Katalog garantiert ein Ergebnis 1 eine Nutzungsdauer von mehr als 30.000 km.
Weitere Überlegungen
Die getrennt berechneten Werte dürfen in keinem Fall den Maximalwert aus dem Katalog überschreiten. Je niedriger dieser Wert ausfällt, umso länger ist die Nutzungsdauer. Wenn Geschwindigkeit und Beschleunigung einen Wert von 3 m/s bzw. 30 m/s2 überschreiten, sollte die Gesamtsumme nicht über 0,7 liegen, sonst ist eine Verkürzung der Nutzungsdauer in Kauf zu nehmen.
WEITERE INFORMATIONEN ZUR LINEAR- UND ROTATIONSTECHNIK IN UNSEREM BLOG
Lassen Sie uns gerne einen Kommentar über die unten aufgeführte Kommentar-Box zukommen. Und wenn es ein Thema gibt, das wir Ihrer Meinung nach ansprechen sollten, lassen Sie es uns bitte wissen.
Wir hoffen, dass die bereitgestellten Informationen hilfreich für Sie sind. Wir empfehlen außerdem, unseren Blog zu abonnieren, damit Sie immer über die neusten Nachrichten und technischen Neuheiten rund um Linearachsen und Co informiert sind.
Wir sehen uns im nächsten Kapitel!
Bis dahin, alles Gute!
Das SINADRIVES Team.









Get Social