Hi mechatronics fans!

Welcome to the latest post on the Sinadrives blog.

June 2022

In this post we’re going to look at some calculations that engineers and designers of industrial machinery need to make in order to improve the performance of machinery. Specifically, we’re going to discuss deflection calculations.

Deflection calculations are required in the case of beams supported at both ends and beams supported at only one end. Let’s take a look at both cases to see how they’re calculated.

Image 1

Deflection calculations are required in the case of beams supported at both ends and beams supported at only one end. Let’s take a look at both cases to see how they’re calculated.

Before discussing the mathematical formula of the calculation, we have to consider how this beam is attached. There are two possibilities: rigid (embedded) attachment or a non-rigid (supported) attachment. In the case of a bridge crane, or a gantry such as the one shown in image 1, the attachment is non-rigid, since there is movement in the X direction.

Image 2 shows a supported beam, while image 3 shows an embedded beam.

Image 2

Image 3

where:
f – deflection, mm
F – point load exerted at the centre of the beam, N
m – total weight of the beam (spread over its entire length), kg
g – gravity acceleration (9.81m/s2)
l – distance between support points, mm
E – modulus of elasticity, N/mm² *
I – geometric inertia moment mm4
The first term corresponds to the point load exerted on the beam; the second term corresponds to the weight of the beam itself.

* The modulus of elasticity for steel is 205,000 N/mm², while that for aluminium is 70,000 N/mm².

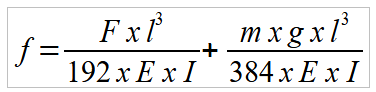
where:
f – deflection, mm
F – point load exerted at the centre of the beam, N
m – total weight of the beam (spread over its entire length), kg
g – gravity acceleration (9.81m/s2)
l – distance between support points, mm
E – modulus of elasticity, N/mm2
I – geometric inertia moment mm4

We can observe that the deflection is between four and five times greater in a supported beam than in an embedded beam.

Image 4 shows a beam supported at one end.

Image 4

In this case, the beam can only have a rigid (embedded) attachment:

f – deflection, mm
F – point load exerted at the free end of the beam, N
m – total weight of the beam (spread over its entire length), kg
g – gravity acceleration (9.81m/s2)
l – distance between support points, mm
E – modulus of elasticity, N/mm2
I – geometric inertia moment mm4

Important:

In addition to the point load exerted on the beam, we must also factor in the effect of the beam’s own weight. In most cases, its own weight generates greater deflection than the load it has to bear.

There’s no set answer to this question; it depends on the application. In the case of a 15-metre bridge crane, for instance, a 100-mm deflection may be acceptable, but in the case of a dynamic gantry, this deflection would be disastrous. As a general rule, we have to consider the following points:

First of all, we must analyse the application and evaluate how the loss of height caused by the deflection may influence the process. For example, in a laser cutting application, a 3-mm deflection may be critical due to the laser’s loss of accuracy. In a water-jet-cutting application, this bending is not as critical.

In this case it’s important to analyse if there’s any vertical movement (a cylinder or a linear actuator) on the bridge (or beam). The larger the deflection, the more elastic the beam becomes and as a result loses rigidity. If the movement of the linear actuator is dynamic, and above all entails constant changes of direction, this may cause the beam to enter a state of resonance. As a general rule, for dynamic applications, the deflection cannot exceed 1 mm and in the case of slow applications it should not exceed 3 mm. These figures should not be taken as a rule; each application requires a detailed study.

On occasions, excessive deflection can generate a series of problems and difficulties for the application. Loss of rigidity, loss of precision, resonances or own frequencies that can compromise the performance of the machinery. The following steps can be taken to reduce deflection:

We can increase the inertia moment by using a beam composed of braces and angle reinforcements (in the style of a construction site crane), instead of using a solid beam. There are a wide variety of standardized steel or aluminium profiles with high inertia values.

Reducing the weight of the beam may also be a good solution. Bending can be reduced by lightening the beam through hollowing it out or by using alternative materials, etc.

The elasticity performance of steel is three times greater than that of aluminium. Deflection can be reduced by using steel. Let’s not forget that in this case the weight will also increase, which means that the goal is to increase the modulus of elasticity in greater proportion than the weight.

If you have an application in which you’re keen to improve the performance of your machine, be it in terms of speed, dynamics, precision or simply reducing maintenance needs, please contact us.

Our specialists in Direct Drive technology and Linear Modules with linear motor technology will be happy to advise you free of charge.

Draw your own conclusions. Decide which innovation you want to implement in your machine to be competitive. We can help you.

Your SINADRIVES Team.